Deli Zhang
- Apr 8, 2015
- 3
- Joined
- Apr 8, 2015
- Messages
- 3
Hi All,
I am back!
In 2008 I posted the thread https://www.electronicspoint.com/thr...ance-ofthe-complex-resistance-network.121263/ and just provided a example. Now I have time to complete the English paper The Formula for the Equivalent Resistance of Complex Resistance Network.pdf as below attachment.
In this paper I given the formula of equivalent resistance for arbitrary circuits and proof. To understand the paper you may have to learn Graph Theory and Metrix Theory, the wording statement of the paper is professional to a mathematics student, even so I will help you understand it.
The example that year took is still the best.
--------------------------------------------------------------------------------
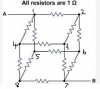
Assuming a four vertices graph (means a circuit with 4 nodes), the conductance between two vertices(it is
symmetric. ):
g(1,2)=1; g(1,3)=2; g(1,4)=3; g(2,3)=4; g(2,4)=5; g(3,4)=6;
The corresponding metrix for the graph:
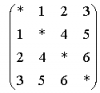
then got the matrix of matrix-tree theory,
M4 =

Attention on the main diagonal elements, which are the sum of all
conductance on the same row and then multiplied by -1
Then, remove the last row and the last column, we get determinant T3.
T3 =
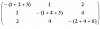
Next, let the conductance g(1,2) between vertex 1 and vertex 2
replaced by number '1', we got T3((g1,2)=1). which is same to T3, because g(1,2)=1 originally.
And let the conductance g(1,2) replaced by number '0', we got
T3(g(1,2)=0) =
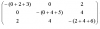
Finally, we get the Equivalent Resistance G(1,2) between vertex 1 and
vertex 2
G(1,2)
= |T3| / (|T3(g(1,2)=1)| - |T3((g(1,2)=0)|)
= (-556) / ((-556)-(-424))
= 139/33
= 4.2121
Equivalent Resistance R(1,2) = 1 / G(1,2) = 0.2374
-------------------------------
Same method, you can get any others,
e.g. G(2,4)
the raw value of g(2,4) is 5, now replaced by 1, so
T3(g(2,4)=1) =
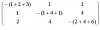
and replaced by 0, got
T3(g(2,4)=0) =
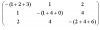
So
G(2,4) = |T3| / (|T3(g(2,4)=1)| - |T3((g(2,4)=0)|)
= (-556) / ((-284)-(-216))
= 139/17
= 8.1765
Equivalent Resistance R(2,4) = 1 / G(2,4) = 0.1223
... ...
Any question, please raise.
Thanks,
Deli
I am back!
In 2008 I posted the thread https://www.electronicspoint.com/thr...ance-ofthe-complex-resistance-network.121263/ and just provided a example. Now I have time to complete the English paper The Formula for the Equivalent Resistance of Complex Resistance Network.pdf as below attachment.
In this paper I given the formula of equivalent resistance for arbitrary circuits and proof. To understand the paper you may have to learn Graph Theory and Metrix Theory, the wording statement of the paper is professional to a mathematics student, even so I will help you understand it.
The example that year took is still the best.
--------------------------------------------------------------------------------
Assuming a four vertices graph (means a circuit with 4 nodes), the conductance between two vertices(it is
symmetric. ):
g(1,2)=1; g(1,3)=2; g(1,4)=3; g(2,3)=4; g(2,4)=5; g(3,4)=6;
The corresponding metrix for the graph:

then got the matrix of matrix-tree theory,
M4 =
Attention on the main diagonal elements, which are the sum of all
conductance on the same row and then multiplied by -1
Then, remove the last row and the last column, we get determinant T3.
T3 =
Next, let the conductance g(1,2) between vertex 1 and vertex 2
replaced by number '1', we got T3((g1,2)=1). which is same to T3, because g(1,2)=1 originally.
And let the conductance g(1,2) replaced by number '0', we got
T3(g(1,2)=0) =
Finally, we get the Equivalent Resistance G(1,2) between vertex 1 and
vertex 2
G(1,2)
= |T3| / (|T3(g(1,2)=1)| - |T3((g(1,2)=0)|)
= (-556) / ((-556)-(-424))
= 139/33
= 4.2121
Equivalent Resistance R(1,2) = 1 / G(1,2) = 0.2374
-------------------------------
Same method, you can get any others,
e.g. G(2,4)
the raw value of g(2,4) is 5, now replaced by 1, so
T3(g(2,4)=1) =
and replaced by 0, got
T3(g(2,4)=0) =
So
G(2,4) = |T3| / (|T3(g(2,4)=1)| - |T3((g(2,4)=0)|)
= (-556) / ((-284)-(-216))
= 139/17
= 8.1765
Equivalent Resistance R(2,4) = 1 / G(2,4) = 0.1223
... ...
Any question, please raise.
Thanks,
Deli