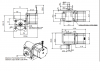
The bipolar geared stepper motor I am planning to use has a resistance/ phase of 8.5 ohms per phase, inductance of 2.14mH per phase , normal current per phase is 2 amps, holding torque of motor is 0.8Nm, gearbox ratio is 1:8, holding torque of gearbox is 6.4Nm. The maximum permissible RPM of gearbox shaft is 200 rpm. The input voltage rating of the stepper motor is 24-48 volts. I am planning to use a 24 volts power supply and DRV8825 driver to drive this motor. Can anyone help me on how to calculate the maximum RPM of the stepper motor ? And also usually how long can the motor run at this maximum speed ?
Also, I intend to use this motor for a motorized cord reel application, where I would retract a cable using this motor and a chain mechanism. The total weight of the cable is around 12 kg. Would this torque of 64kgcm (6.4Nm) be sufficient for this application?
The diameter of the cable drum is 100mm, and the diameter of the cable is 18mm, with the length of the cable being 29 feet
Attached datasheet of motor here:
Also, I intend to use this motor for a motorized cord reel application, where I would retract a cable using this motor and a chain mechanism. The total weight of the cable is around 12 kg. Would this torque of 64kgcm (6.4Nm) be sufficient for this application?
The diameter of the cable drum is 100mm, and the diameter of the cable is 18mm, with the length of the cable being 29 feet
Attached datasheet of motor here:
Attachments
Last edited: