Solution to this op amp circuit

[Dan_DG]

Like my previous post, I need to find the transfer function for the following op amp. However this question is a little bit more difficult. I honestly have no idea where to start (I'm not sure if that's just because it is really late), but could someone just give me a push in the right direction. I know I am missing something really simple but I just can't seem to figure out what.

 

[LvW]

Dan, like always - there are some different ways to solve the task.
That means, you can start at "zero" with equations derived from basic laws (KVL and KCL) or you can start - for example - with the classical equation for feedback.
I prefer this way because it is straight-forward and relatively simple (and logical).

1.) The basic formula for the closed-loop gain of a circuit with feedback is Acl=Hf*Aol/(1-Aol*Hr) = Hf/(1/Aol - Hr).
Aol: Open-loop gain of the opamp, Hr: Feedback factor (sometimes also called "beta", Hf: Forward damping factor.

2.) Definitions:
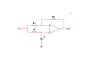
Hf=(Vp-Vn) for Vout=0 and Hr=(Vp-Vn) for Vin=0. (Vp, Vn: voltages at the pos. resp. negative opamp input nodes).
For negative feedback (usual case) this leads to a negative feedback factor Hr.

3.) Assumng Aol to be infinite, we have: Acl=-Hf/Hr

4.) Now, you can separately compute Hf and Hr (simple voltage divider rules) and find the ratio.

This method has the advantage that you have divided the whole calculation task in two separate steps.
Try also to find the solution for three equal resistors. It is the transfer function for a well-known filter circuit.

 

[Laplace]

The advantage of any particular method must be a matter of opinion, and we all have our opinion. Start with the node equations; it is a simple mechanical process to write node equations, with no conceptualizing about how to apply the feedback equation to your circuit.

Then realize that both op amp input terminals are at the same voltage. Vop+ = Vop- = Vop (Negative feedback makes it so.)

So there are two nodes and two node equations:

(Vop-Vin)/R1 + (Vop-Vout)/R2 = 0

(Vop-Vin)/R + Vop/(1/(s*C)) = 0

Solve for Vop in each node equation, set Vop=Vop, solve for Vout/Vin. It is a simple plug & chug solution with little chance of making conceptual errors, whereas I would not have any confidence in a solution I derived by starting with the feedback equation, exhibiting implicit trust in my ability to make conceptual errors.

 

[LvW]

I would not have any confidence in a solution I derived by starting with the feedback equation, .........

Since Blacks formula for a system with feedback has proven to be correct (many decades ago), I see no reason not to "have any confidence".
Hi Laplace - please, can you justify your criticism? Can you explain why this way to solve the task is not trustworthy?
It is just an application of the well-known superposition theorem.

 

[Laplace]

Can you explain why this way to solve the task is not trustworthy?

It was not a criticism. I thought it was clear that I did not consider myself trustworthy to correctly apply the theorem. So over the years I have found it best to approach circuit analysis with a consistent method: the node equations. I seldom make conceptual errors when writing the node equations (unlike other methods), and use a symbolic algebra program to chug through the math. Using the node equations in this way is a reliable method because the opportunity for making mistakes is minimal, at least in my experience.

 

[LvW]

Using the node equations in this way is a reliable method because the opportunity for making mistakes is minimal, at least in my experience.

I am sure one could discuss about this - but this wouldn´t make much sense in the context of this thread.
As you have said before: It is a "matter of opinion, and we all have our opinion."