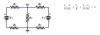
First off, this is KCL so starting with loop currents is a mistake.
Kirchoffs Current Law or KCL, states that the “total current or charge entering a junction or node is exactly equal to the charge leaving the node as it has no other place to go except to leave, as no charge is lost within the node“. In other words the algebraic sum of ALL the currents entering and leaving a node must be equal to zero. (
http://www.electronics-tutorials.ws/dccircuits/dcp_4.html)
So KCL sums the current at a node in terms of the node voltage and the resistance to adjacent nodes. The first task then is to identify the nodes and the voltages at each node. But voltages are measured with respect to a reference, so one of the nodes must be designated the ground node. However, this problem has a complication: multiple voltage sources. The voice of experience says that the equations will be more elegant if the series junction of a single resistor and voltage source is not identified as a node. Of course, it can be a node but then one must write an additional constraint equation. With that said, this problem has only one node; therefore, only one node equation.
To demonstrate how the node equation is written, I'll use a slightly different circuit. Note that when writing the individual node currents, it was most convenient to just mentally exchange the position of V1 & R4 and V2 & R5.