Connect with us

Calculating current through resistors

Reply to Thread

Discussion in 'Electronics Homework Help' started by Diar, Nov 7, 2014.

Scroll to continue with content
  1. Nov 7, 2014 #1
    Diar

    Diar

    12
    1
    Jul 27, 2014
    IMG_1927.JPG

    Ok so I'm pretty new to electronics. Taking a part time course one day a week and trying to fit it in with working 60 hours a week. My lecturer moves through things pretty quickly and the rest of the class have a background so I'd rather not hold them back with my pretty basic questions seeing as its a higher level course (don't ask how i managed to blag my way onto it).
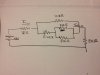
    So I'm stuck trying to calculate the current through I1 and I5 in this circuit, I've worked out the total resistance for the circuit and the total current, I just cant figure out how to calculate current through these points, its just not clicking for me.
     
  2. Nov 8, 2014 #2
    Gryd3

    Gryd3

    4,098
    875
    Jun 25, 2014
    Remember that the current through components in series will be the same.
    Voltage across components in parallel will be the same.

    We can make the observation that your complicated resistor network can be looked at as 3 resistors in series. You have the first resistor where I1 is located, then you have your small network of parallel resistors which can be looked at as a single aggregate resistor, then you have the last resistor. I5 is the current flowing into the last resistor. Now because these points are in series, we can say that I1 and I5 will be the same. We can also determine the current flow through the circuit because you have calculated the total resistance of the circuit yes?
    Once you know the total resistance, you can calculate the total current through your circuit. Like I stated above, all current will be the same through a series portion of the circuit. Once you connect the dots, you'll have your answer.
     
    chopnhack likes this.
  3. Nov 8, 2014 #3
    chopnhack

    chopnhack

    1,573
    352
    Apr 28, 2014
    Agreed, the group in the center is nothing more than nested parallel resistors that can get resolved down to an equivalent resistance. Can anyone show the math to distribute the voltage drop to each individual resistor in the parallel network?

    upload_2014-11-7_20-18-2.png
     
    Last edited: Nov 8, 2014
    Arouse1973 likes this.
  4. Nov 11, 2014 #4
    Diar

    Diar

    12
    1
    Jul 27, 2014
    When you are calculating out your resistances are you taking into consideration they are k ohm? So it would be 1.6k and 3k ohm. Giving a final current of 0.001A and not 1A as you have stated?
     
  5. Nov 11, 2014 #5
    Harald Kapp

    Harald Kapp Moderator Moderator

    10,218
    2,201
    Nov 17, 2011
    From your original schematic it is hard to recognize that the values are in kΩ.
    Be that as it may: yes, scaling up all resistors from Ω to kΩ will schale down the currrent accordingly from A to mA.
     
  6. Nov 11, 2014 #6
    Diar

    Diar

    12
    1
    Jul 27, 2014
    My handwriting is pretty awful to be fair!
     
    Gryd3 likes this.
  7. Nov 12, 2014 #7
    chopnhack

    chopnhack

    1,573
    352
    Apr 28, 2014
    Sorry, I thought it was unconventional to write 1RΩ, LOL, but didn't think that it was 1kΩ! o_O;)
     
    davenn likes this.
  8. Nov 12, 2014 #8
    davenn

    davenn Moderator

    13,618
    1,882
    Sep 5, 2009
    yeah me too
     
  9. Nov 12, 2014 #9
    (*steve*)

    (*steve*) ¡sǝpodᴉʇuɐ ǝɥʇ ɹɐǝɥd Moderator

    25,411
    2,779
    Jan 21, 2010
    Whilst the equation for parallel resistors R = (R1 * R2) / (R1 + R2) is kinda simple and easy to remember, I find 1/R = 1/R1 + 1/R2 easier to actually apply, and it is far better illustrative of the sometimes useful concept of dealing with conductance rather than resistance.
     
    chopnhack and KrisBlueNZ like this.
  10. Nov 12, 2014 #10
    chopnhack

    chopnhack

    1,573
    352
    Apr 28, 2014
    Can you elaborate further Steve?
     
  11. Nov 13, 2014 #11
    (*steve*)

    (*steve*) ¡sǝpodᴉʇuɐ ǝɥʇ ɹɐǝɥd Moderator

    25,411
    2,779
    Jan 21, 2010
    Conductance = 1 / resistance

    If we look at resistors in series, the total resistance is the sum of each individual resistance.

    If we look at resistors in parallel, the total conductance is the sum of the conductances for each resistor.

    The equation using the product divided by the sum produces the same result as the reciprocal of the sum of the reciprocals. The former method is also easier with slide rules, tables of logarithms, and maybe even for pencil and paper.

    However the latter method reinforces the resistance/conductance aspect, is easier to rearrange to find another resistor in parallel to give a desired total resistance, and can be easier to do in your head (well it is for me).

    If you find yourself with an equation using lots of resistances in the denominator, it can be a useful simplification to convert these to conductances.

    The other thing is that its hard to get wrong. The product over sum can be easily misremembered as sum over product, yielding an incorrect result.
     
    chopnhack, KrisBlueNZ and Gryd3 like this.
Ask a Question
Want to reply to this thread or ask your own question?
You'll need to choose a username for the site, which only take a couple of moments (here). After that, you can post your question and our members will help you out.
Similar Threads

  1. Calculating current flowing through a circuit and voltage drop?!

  2. Calculating resistance and Base current

  3. Power through current sources

  4. Calculating V

  5. Resistors

  6. Resistors

  7. Calculating resolution.

  8. Calculating reflection coefficient

Loading...
Electronics Point Logo
Continue to site
Quote of the day

“”

-