Hello folks,
I have a really simple problem.
I'm probing the input current peak of a system and I'd like to calculate the equivalent power consumption.
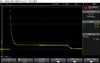
This peak current is about 3.3A for 2ms approximately and the system is powered by a 12V power-supply. The signal form is not exactly this one but I simplified it for the sake of the exercise. I attached the screenshot of the real one to this post (and before you ask, the unit is actually in A, but I forgot to change the unit in the oscilloscope).
If the peak lasted 1s it would be simple and I would only have to write the traditional equation P = I x V = 3.3A x 12V = 39.6W. But as this peak last only 2ms, then it cannot be that high.
Then, I would have written something like (3.3A x 2ms) x 12V... However, it would not define a power anymore, but an energy, unless I say it is a normalization to 1s like in the following formula:
Did I write this equation right?
I acquired the value samples from an oscilloscope to calculate the power by transcripted the equation in the discrete-domain. Here is how I computed it:

With N the number of sample during the peak and M the total number of sample during 1s.
I considered Vn and Vm as constants equals to 12V since the voltage value barely changed during the current peak.
However, summing the first part of the equation (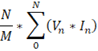 ) already gives me a result too high to be realistic.
) already gives me a result too high to be realistic.
Indeed, in my example I have M = 10^5 samples, N = 127 sample and sum(VnxIn) = 1700W.
Then it gives a result of 2.16W, for only 2ms (while it has to be 39.6W for a full second).
I am a little bit confused and lost in my equations right now... Could you please help me solve this issue? Otherwise, could you please give me some advices or document I could read to learn more about this subject?
Thanks a lot for your help!
I have a really simple problem.
I'm probing the input current peak of a system and I'd like to calculate the equivalent power consumption.
This peak current is about 3.3A for 2ms approximately and the system is powered by a 12V power-supply. The signal form is not exactly this one but I simplified it for the sake of the exercise. I attached the screenshot of the real one to this post (and before you ask, the unit is actually in A, but I forgot to change the unit in the oscilloscope).
If the peak lasted 1s it would be simple and I would only have to write the traditional equation P = I x V = 3.3A x 12V = 39.6W. But as this peak last only 2ms, then it cannot be that high.
Then, I would have written something like (3.3A x 2ms) x 12V... However, it would not define a power anymore, but an energy, unless I say it is a normalization to 1s like in the following formula:
Did I write this equation right?
I acquired the value samples from an oscilloscope to calculate the power by transcripted the equation in the discrete-domain. Here is how I computed it:
With N the number of sample during the peak and M the total number of sample during 1s.
I considered Vn and Vm as constants equals to 12V since the voltage value barely changed during the current peak.
However, summing the first part of the equation (
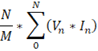 ) already gives me a result too high to be realistic.
) already gives me a result too high to be realistic.Indeed, in my example I have M = 10^5 samples, N = 127 sample and sum(VnxIn) = 1700W.
Then it gives a result of 2.16W, for only 2ms (while it has to be 39.6W for a full second).
I am a little bit confused and lost in my equations right now... Could you please help me solve this issue? Otherwise, could you please give me some advices or document I could read to learn more about this subject?
Thanks a lot for your help!